Cálculo diferencial El cálculo fue inventado por Newton y Leibniz en el siglo XVII como resultado de una gran cantidad de trabajo matemático que condujo al estudio de los derivados, tangentes a curvas y lo infinitamente pequeño. Este cálculo fue desarrollada posteriormente por varios matemáticos (Euler, Laplace, Cauchy, ...), que dio su forma actual.
Ya era el álgebra antes de Cristo y el famoso Arquímedes sabía cómo resolver ciertas ecuaciones de 2 º grado, uno debe aceptar que, siempre y cuando no fue hasta la llegada de Leibnitz y Newton, tres cien años solamente, es que este cálculo es sutil y trascendente, y un nivel superior a las matemáticas elementales.
Lo infinitamente pequeño. Una infinitesimal es una cantidad variable que tiende a 0.
Ejemplos
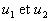 son equivalentes si el límite infinitesimal de la relación
son equivalentes si el límite infinitesimal de la relación 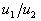 tiende a 1 cuando
tiende a 1 cuando 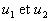 tienden a 0.
tienden a 0.
Se verá, por ejemplo, que lo infinitamente pequeño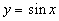 es equivalente a la x muy pequeños, o de lo infinitamente pequeño
es equivalente a la x muy pequeños, o de lo infinitamente pequeño 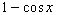 es equivalente a
es equivalente a 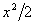
differential calculus
The calculation was invented by Newton and Leibniz in the seventeenth century as a result of a lot of mathematical work that led to the study of derivatives, tangents to curves and the infinitely small. This calculation was further developed by several mathematicians (Euler, Laplace, Cauchy, ...), which gave its present form.
It was the algebra BC and the famous Archimedes knew how to solve certain equations of grade 2, one must accept that as long as it was not until the arrival of Leibnitz and Newton, three hundred years alone, is that this calculation is subtle and transcendent, and a higher level of elementary mathematics.
The infinitely small. An infinitesimal is a variable quantity tends to 0.
Ya era el álgebra antes de Cristo y el famoso Arquímedes sabía cómo resolver ciertas ecuaciones de 2 º grado, uno debe aceptar que, siempre y cuando no fue hasta la llegada de Leibnitz y Newton, tres cien años solamente, es que este cálculo es sutil y trascendente, y un nivel superior a las matemáticas elementales.
Lo infinitamente pequeño. Una infinitesimal es una cantidad variable que tiende a 0.
Ejemplos
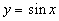 cuando x tiende a 0 cuando tiende a 0, por lo que este es un infinitamente pequeño
cuando x tiende a 0 cuando tiende a 0, por lo que este es un infinitamente pequeño
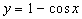 cuando x tiende a 0 cuando tiende a 0, por lo que este es un infinitamente pequeño.
cuando x tiende a 0 cuando tiende a 0, por lo que este es un infinitamente pequeño.
Se verá, por ejemplo, que lo infinitamente pequeño
differential calculus
The calculation was invented by Newton and Leibniz in the seventeenth century as a result of a lot of mathematical work that led to the study of derivatives, tangents to curves and the infinitely small. This calculation was further developed by several mathematicians (Euler, Laplace, Cauchy, ...), which gave its present form.
It was the algebra BC and the famous Archimedes knew how to solve certain equations of grade 2, one must accept that as long as it was not until the arrival of Leibnitz and Newton, three hundred years alone, is that this calculation is subtle and transcendent, and a higher level of elementary mathematics.
The infinitely small. An infinitesimal is a variable quantity tends to 0.

Comments