Ecuaciones diferenciales de segundo orden
Sólo las ecuaciones diferenciales de segundo orden lineales con coeficientes constantes con RHS que realmente nos interesa, oLos resultados de la linealidad
En cuanto al segundo término, corrió a casos reales, como una constante, un poder polinomio de x, o una combinación lineal de coseno y seno del grupo
Buscamos, respectivamente, para la solución particular, una constante, un polinomio de grado 2 en el poder de x, una combinación lineal de coseno y seno del grupo
Sustituyendo, se forma la ecuación característica
Al explicar los siguientes valores
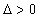 ð
ð 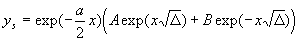
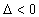 ð
ð 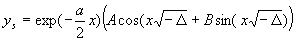
 ð
ð 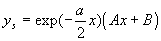
Differential equations
Only the differential equations of second order linear with constant coefficients with RHS we're really interested, or
The linearity results
Regarding the second term, he ran to real cases, as a constant, a polynomial power of x or a linear combination of cosine and sine of the group
We search respectively, for the particular solution, a constant, a polynomial of degree 2 in power of x, a linear combination of cosine and sine of the group
Substituting, we form the characteristic equation
By explaining the following values
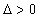 ð
ð 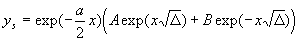
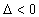 ð
ð 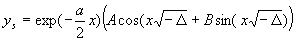
 ð
ð 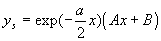

Comments