Ecuaciones diferenciales, en general,Differential equations, general

Ecuaciones diferenciales, en general:

El concepto de diferencial de Leibniz permite resolver ecuaciones funcionales (la incógnita es una función) que aparecen como la variable x de la función y = f (x) y / o algunos de sus derivados "y = (X), y "= (X) la función derivada de Y así sucesivamente.

El más básico es de la forma A (x) = y'B (y) por separación de variables: el diferencial promedio, y 'se puede escribir como dy / dx y tal ecuación es de la forma:

A (x) dx = B (y) dy

por lo tanto, la ecuación diferencial nombre. Mediante la integración de ambos lados:

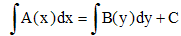
Una ecuación como A (x) y '+ B (x) y = 0 es un caso especial de la ecuación lineal

Differential equations, general:

The concept of differential allows Leibniz to solve functional equations (the unknown is a function) which appear as the variable x the function y = f (x) and / or some of its derivative y '= 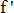(X), y "= 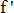(X) function derived from 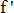And so on.

The most basic is of the form A (x) = y'B (y) by separation of variables: the average differential, y 'can be written as dy / dx and such an equation is of the form:

A (x) dx = B (y) dy

hence the name differential equation. By integrating both sides:

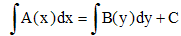
An equation such as A (x) y '+ B (x) y = 0 is a special case of elementary linear equation